本文转自https://www.cnblogs.com/of-fanruice/p/7678801.html
归并排序 (merge sort) 是一类与插入排序、交换排序、选择排序不同的另一种排序方法。归并的含义是将两个或两个以上的有序表合并成一个新的有序表。归并排序有多路归并排序、两路归并排序 , 可用于内排序,也可以用于外排序。这里仅对内排序的两路归并方法进行讨论。
一、两路归并排序算法思路
分而治之(divide - conquer);每个递归过程涉及三个步骤
第一, 分解: 把待排序的 n 个元素的序列分解成两个子序列, 每个子序列包括 n/2 个元素.第二, 治理: 对每个子序列分别调用归并排序MergeSort, 进行递归操作第三, 合并: 合并两个排好序的子序列,生成排序结果.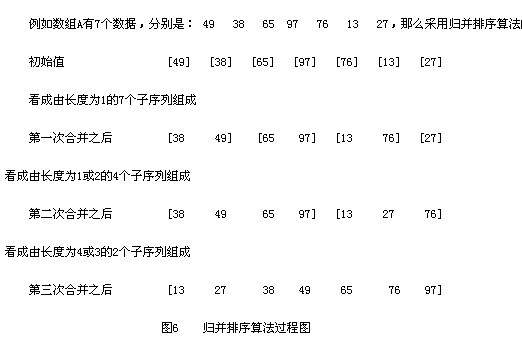
二、算法实现
此算法的实现不像图示那样简单,现分三步来讨论。首先从宏观上分析,首先让子表表长 L=1 进行处理;不断地使 L=2*L ,进行子表处理,直到 L>=n 为止,把这一过程写成一个主体框架函数 mergesort 。然后对于某确定的子表表长 L ,将 n 个记录分成若干组子表,两两归并,这里显然要循环若干次,把这一步写成一个函数 mergepass ,可由 mergesort 调用。最后再看每一组(一对)子表的归并,其原理是相同的,只是子表表长不同,换句话说,是子表的首记录号与尾记录号不同,把这个归并操作作为核心算法写成函数 merge ,由 mergepass 来调用。假设我们有一个没有排好序的序列,那么首先我们使用分割的办法将这个序列分割成一个一个已经排好序的子序列,然后再利用归并的方法将一个个的子序列合并成排序好的序列。分割和归并的过程可以看下面的图例。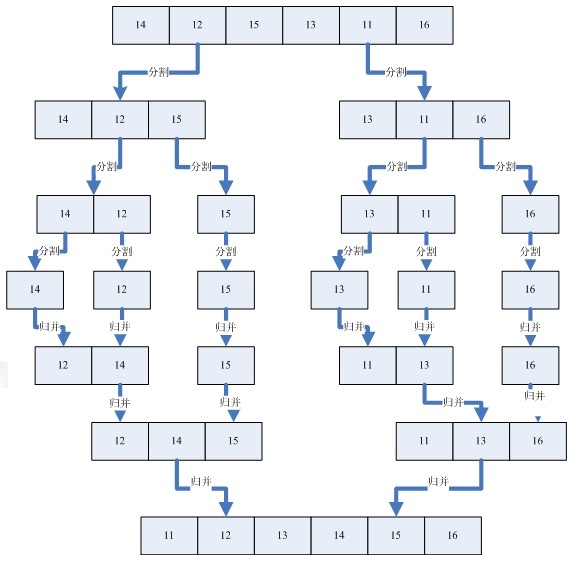
三、代码实现
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | public static int [] sort( int [] a, int low, int high){ int mid = (low+high)/ 2 ; if (low<high){ sort(a,low,mid); sort(a,mid+ 1 ,high); //左右归并 merge(a,low,mid,high); } return a; } public static void merge( int [] a, int low, int mid, int high) { int [] temp = new int [high-low+ 1 ]; int i= low; int j = mid+ 1 ; int k= 0 ; // 把较小的数先移到新数组中 while (i<=mid && j<=high){ if (a[i]<a[j]){ temp[k++] = a[i++]; } else { temp[k++] = a[j++]; } } // 把左边剩余的数移入数组 while (i<=mid){ temp[k++] = a[i++]; } // 把右边边剩余的数移入数组 while (j<=high){ temp[k++] = a[j++]; } // 把新数组中的数覆盖nums数组 for ( int x= 0 ;x<temp.length;x++){ a[x+low] = temp[x]; } } |
四、算法分析
(1)稳定性
归并排序是一种稳定的排序。(2)存储结构要求 可用顺序存储结构。也易于在链表上实现。(3)时间复杂度 对长度为n的文件,需进行趟二路归并,每趟归并的时间为O(n),故其时间复杂度无论是在最好情况下还是在最坏情况下均是O(nlgn)。(4)空间复杂度 需要一个辅助向量来暂存两有序子文件归并的结果,故其辅助空间复杂度为O(n),显然它不是就地排序。 注意: 若用单链表做存储结构,很容易给出就地的归并排序